Deformations and Distortions

Sometimes, it makes sense to see what a function does to curves or surfaces from the domain space.  So, for example:

polarTransform[{u_, v_}] := {u Sin[v], u Cos[v]}

domainCurveU = {t, π/6} ; domainCurveV = {1, t} ;

This graphs these two lines in the domain space (the green one holds u constant and varies v, while the red one reverses this).

domainCurves = ParametricPlot[{domainCurveU, domainCurveV}, {t, -5, 5}, PlotStyle {Red, Green}, AspectRatioAutomatic]

[Graphics:../HTMLFiles/index_163.gif]

⁃Graphics⁃

Our function transforms these two curves as follows:

polarTransform[domainCurveU]

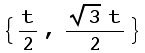
{t/2, (3^(1/2) t)/2}

polarTransform[domainCurveV]

{Sin[t], Cos[t]}

rangeCurves = ParametricPlot[Evaluate[{polarTransform[domainCurveU], polarTransform[domainCu ... ectRatioAutomatic, PlotStyle {Red, Green}, PlotRange {{-5, 5}, {-5, 5}}]

[Graphics:../HTMLFiles/index_170.gif]

⁃Graphics⁃

(With a little more work, you could construct a grid of these and see how it transforms in general.)  Here's another example with a less common function:

fTransform[{u_, v_}] := {u + v, u^2/v^2}

domainCurveU = {t, 1} ; domainCurveV = {1, t} ;

domainCurves = ParametricPlot[{domainCurveU, domainCurveV}, {t, -5, 5}, PlotStyle {Red, Green}, AspectRatioAutomatic]

[Graphics:../HTMLFiles/index_175.gif]

⁃Graphics⁃

fTransform[domainCurveU]

{1 + t, t^2}

fTransform[domainCurveV]

{1 + t, 1/t^2}

rangeCurves = ParametricPlot[Evaluate[{fTransform[domainCurveU], fTransform[domainCurveV]}], ... ectRatioAutomatic, PlotStyle {Red, Green}, PlotRange {{-5, 5}, {-5, 5}}]

[Graphics:../HTMLFiles/index_182.gif]

⁃Graphics⁃

Problem

Problems:
For each of the following functions, decide upon a suitable method to display the graph (using the techniques mentioned above or other appropriate methods) and use Mathematica to show it. Warning:  The fanciest method is definitely not always the best choice.  Choose ANY THREE of these to do.

1.  T(x,y,t)=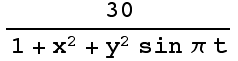30/(1 + x^2 + y^2sin π t)
T - The temperature (in °C) on the surface of a flat plate t hours after midnight at the point (x,y) (both measured in inches from the center).

2.  L(x,y)=<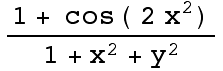(1 + cos ( 2x^2))/(1 + x^2 + y^2),20sin^2(x y)>
L - The surface mass density (first coordinate of the range, in kg/m^2) and temperature (second coordinate of the range, in °C) at a point (x,y) on a plane.

3.  Overscript[∇, ]·polarTransform(u,v)
This is the same polarTransform function I defined in the explanatory text (above).

4.  Cy(u,v,w)=<-u cos v,-u sin v,w>
Do this one twice.  Once, consider that this gives the velocity vector field of a fluid.  Now, consider it as a transformation (or "change of coordinates") and graph it.

5.  D(u,v,t)=<u (cos v) (1+cos t),u (sin v)(1+ sin t)>
This is a change of coordinates that is time-dependent.

Created by Mathematica  (February 28, 2007) Valid XHTML 1.1!