calculus_IV_lab

Integration

Path integrals

If you need to integrate a scalar-valued function over a curve, it is pretty straight-forward. For example, to integrate over the curve , you need to simply use ArcLengthFactor to convet ds to dt and compose f and c:

$f[{x_, y_, z_}] := x^2y^3^z$

$c[t_] := {t, Sin[t], Tan[t]}$

NIntegrate[f[c[t]] ArcLengthFactor[c[t], t, Cartesian], {t, 0, π/4}]

If your curve (and function) is in some other coordinate system, you simply have to specify that in the ArcLengthFactor term. (Be careful that you specify your variables in the order Mathematica expects them in for your coordinate system, both in f and in c.)

Problem

Triple integrals

When working a triple integral, you sometimes have to work in alternate coordinate systems. You can use some of the techniques from above to make the computations easier.

For example, if you had to do the following integral:

Underscript[∫∫∫, R] x^3 (x^2 + y^2)^(1/2) V , where R is the region defined by $R = {(r, θ, z} 1≤u≤v^2, 2≤v≤3, 0≤ϕ≤π/6}$ in Paraboloidal coordinates.

First, let's examine the region by graphing each of the boundaries (this is a pain, but I haven't thought of a faster method yet):

faceULo = ParametricPlot3D[Evaluate[CoordinatesToCartesian[{1, v, ϕ}, Paraboloidal]], {v, 2, 3}, {ϕ, 0, π/6}]

-Graphics3D-

$faceUHi = ParametricPlot3D[Evaluate[CoordinatesToCartesian[{v^2, v, ϕ}, Paraboloidal]], {v, 2, 3}, {ϕ, 0, π/6}]$

-Graphics3D-

faceVLo = ParametricPlot3D[Evaluate[CoordinatesToCartesian[{u, 2, ϕ}, Paraboloidal]], {u, 1, 9}, {ϕ, 0, π/6}]

$General :: spell1 : Possible spelling error: new symbol name \"faceVLo\" is similar to existing symbol \"faceULo\". More…$

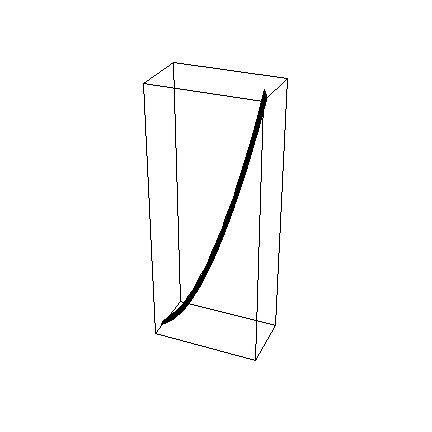
-Graphics3D-

faceVHi = ParametricPlot3D[Evaluate[CoordinatesToCartesian[{u, 3, ϕ}, Paraboloidal]], {u, 1, 9}, {ϕ, 0, π/6}]

$General :: spell1 : Possible spelling error: new symbol name \"faceVHi\" is similar to existing symbol \"faceUHi\". More…$

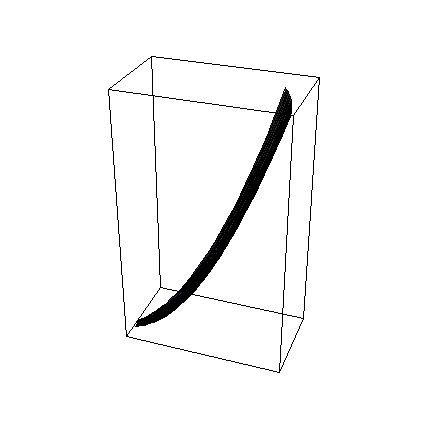
-Graphics3D-

faceϕLo = ParametricPlot3D[Evaluate[CoordinatesToCartesian[{u, v, 0}, Paraboloidal]], {u, 1, 9}, {v, 2, 3}]

-Graphics3D-

faceϕHi = ParametricPlot3D[Evaluate[CoordinatesToCartesian[{u, v, π/6}, Paraboloidal]], {u, 1, 9}, {v, 2, 3}]

-Graphics3D-

Actually, let's leave off one of the sides (which face is that?):

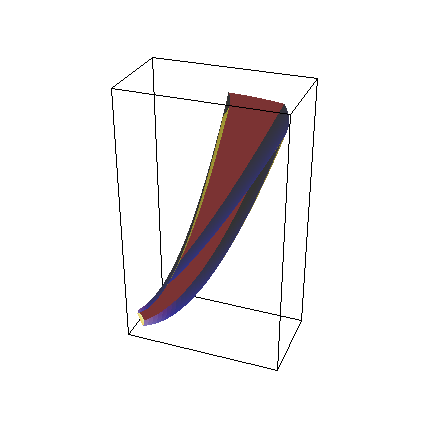
-Graphics3D-

So, not a great candidate for integration in Cartesian coordinates. (It's the region on the inside.) Let's convert everything into Paraboloidal:

$fCartesian[{x_, y_, z_}] := x^3 (x^2 + y^2)^(1/2)$

$fParaboloidal[{u_, v_, ϕ_}] = fCartesian[CoordinatesToCartesian[{u, v, ϕ}, Paraboloidal[u, v, ϕ]]]//FullSimplify$

$General :: spell1 : Possible spelling error: new symbol name \"fParaboloidal\" is similar to existing symbol \"Paraboloidal\". More…$

$General :: spell1 : Possible spelling error: new symbol name \"jDet\" is similar to existing symbol \"Det\". More…$

$∫_0^(π/6) ∫_2^3∫_1^v^2fParaboloidal[{u, v, ϕ}] jDetuvϕ$

Problem

Created by Mathematica (October 18, 2004)