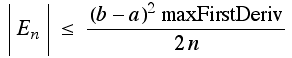numerical_integration

Error approximation for the Left/Right sums

In order to find an error bound for these approximations, it can be shown that the maximum error is given by 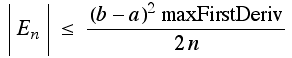E_n≤ ((b - a)^2maxFirstDeriv)/(2n) , where maxFirstDeriv is the maximum size of the first derivative on the interval . To compute this, let's make some definitions:

(x Cos[x^2])/(1 + Sin[x^2])^(1/2)

You can use Mathematica's FindMinimum function to find the minimum and maximum values of the derivative over the interval, but this may miss a critical point (or an endpoint) in some cases, so it is a really good idea to look at a graph of the derivative over to check that you got the correct value. (If you aren't too particular, you could use the trace tool to find the approximate coordinates strictly from the graph. Click once on the graph, then move the mouse over the graph while holding down the Control key. The coordinates of the mouse cursor are shown at the lower left edge of this window. Not very accurate, but fast...)

[Graphics:../HTMLFiles/index_22.gif]

To get more accuracy, we need to compare 4 different values: FindMinimum of firstDeriv, FindMinimum of (Mathematica doesn't have a "FindMaximum" command, oddly enough), , and . The largest one of these will be the maximum. (If you know that your function is simple enough, there are snazzier ways to do this, but this works.) The FindMinimum command I use below starts looking at and looks throughout the interval .

This doesn't find anything because there are no local minima to find (it doesn't look for endpoints usually). Now let's check for a maximum:

We do get an answer here (notice that it has the wrong sign; it actually occurs at 0.512394). Now, let's compare this with the endpoints and pick the maximum size (hence the absolute values). The notation is used to pull just the y value out (and ignores the x value).

Max[Abs[{localMin[[1]], localMax[[1]], firstDeriv[a], firstDeriv[b]}]]//N

$RowBox[{Max, [, RowBox[{0.962853, ,, RowBox[{Abs, [, RowBox[{(x Cos[x^2]), /, RowBox[{RowBox[{(, RowBox[{RowBox[{1., }], +, Sin[x^2]}], )}], ^, (1/2)}]}], ]}]}], ]}]$

Since strange things like the symbolic answer above sometimes come up, I will just copy and paste the answer to the following definition (note that you need to change this if you change the function or the interval).

This defines a function that computes the error bound for n rectangles:

maxLRError[n_] := ((b - a)^2maxFirstDeriv)/(2n)

Compare how the error bounds ("Max error") change as you increase the number of subdivisions below:

TableForm[Table[{n, leftSum[n], maxLRError[n], Abs[leftSum[n] - actualValue]}, {n, 100, 1000, ... #62754; {None, {"n", "LHS", "Max error", "Actual error"}}]

LHS

Max error

Actual error

100

1.9248595511698364134

0.0118787

0.0021754557898253107

200

1.9259522284001378183

0.00593936

0.0010827785595239058

300

1.9263142544597990703

0.00395958

0.0007207524998626538

400

1.9264948550389291754

0.00296968

0.0005401519207325487

500

1.9266030834013952095

0.00237575

0.0004319235582665146

600

1.9266751806491492182

0.00197979

0.0003598263105125059

700

1.9267266517474423757

0.00169696

0.0003083552122193484

800

1.9267652403406265361

0.00148484

0.0002697666190351880

900

1.9267952449616704353

0.00131986

0.0002397619979912888

1000

1.9268192431591012223

0.00118787

0.0002157638005605018

The table above shows the number of subdivisions increased by an order of magnitude. Explain how the error bound changes as a result of this. Do you expect this to hold true for other functions and/or intervals of integration as well? Why or why not?

How does the error bound compare to the actual error in this table? Do you expect that relationship to be the same if you are integrating some other function? Why or why not? Does it decrease in the same way that the error bound does as you increase the number of subdivisions? Does this depend on the specific function used?

We can also graph the error bound as a function of the number of subdivisions (holding everything else constant):

[Graphics:../HTMLFiles/index_47.gif]

What general conclusions can you draw about the accuracy and "efficiency" of the left-hand and right-hand sums in computing an integral? For the given integral, where would you say your point of "diminishing returns" would be reached (i.e., if you increase the number of subdivisions above this point, you have to work really hard to get just a little more accuracy)? If you stopped there, how accurate would your integral be?

Created by Mathematica (April 22, 2004)